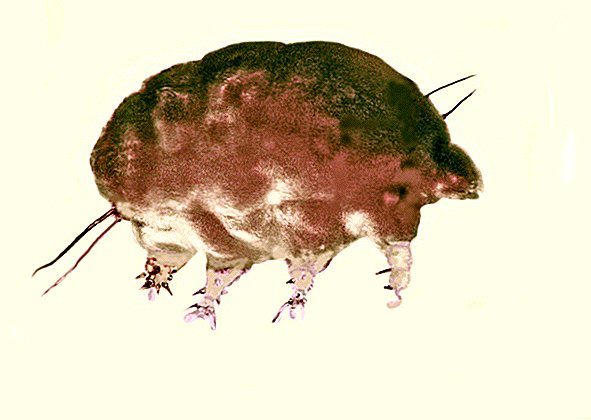
Título: Vista de la luna en perigeo y apogeo
Como docente, siempre estoy buscando laboratorios con configuraciones simples apropiadas para los estudiantes. Mi favorito actual es encontrar la velocidad de la luz con el chocolate.
En un nuevo artículo recientemente subido a arXiv, Kevin Krisciunas de Texas A&M describe un método para determinar la excentricidad orbital de la luna con un error sorprendentemente bajo usando nada más que un metro, un trozo de cartón y un programa destinado a ajustar curvas a estrellas variables
Este método hace uso del hecho de que la excentricidad se puede determinar a partir de la relación del tamaño angular medio de un objeto y la mitad de su amplitud. Por lo tanto, el objetivo principal es medir estas dos cantidades.
La estrategia de Kevin para hacer esto es hacer uso de un orificio de observación de cartón que puede deslizarse a lo largo de un metro. Mirando a través del agujero hacia la luna y deslizando la tarjeta de un lado a otro hasta que el tamaño angular del agujero se superponga a la luna. A partir de ahí, el diámetro del agujero dividido por la distancia hacia abajo del medidor da el tamaño angular gracias a la fórmula de ángulo pequeño (? = D / D en radianes si D >> d).
Para evitar errores sistemáticos al juzgar mal a medida que la tarjeta se desliza hacia adelante hasta que el tamaño del agujero coincida con la luna, es mejor acercarse también desde la otra dirección; Viniendo desde el otro extremo del medidor. Esto debería ayudar a reducir los errores y, en el intento de Kevin, descubrió que tenía una extensión típica de ± 4 mm al hacerlo.
En este punto, todavía hay otro error sistemático que debe tenerse en cuenta: la pupila tiene un tamaño finito comparable al agujero de observación. Esto hará que se subestime el tamaño angular real. Como tal, es necesario un factor de corrección.
Para derivar este factor de corrección, Kevin colocó un disco de 91 mm a una distancia de 10 metros (esto debería producir un disco con el mismo tamaño angular que la luna cuando se ve desde esa distancia). Para producir la mejor combinación, el deslizamiento de cartón con el orificio de observación debería necesita colocarse a 681.3 mm en el medidor, pero debido al error sistemático de la pupila, Kevin descubrió que debía colocarse a 821 mm. La relación entre la ubicación observada y la ubicación adecuada proporcionó el factor de corrección que Kevin utilizó (1.205). Esto necesitaría ser calibrado para cada persona individual y también dependería de la cantidad de luz durante el tiempo de observación ya que esto también afecta el diámetro de la pupila. Sin embargo, adoptar un único factor de corrección produce resultados satisfactorios.
Esto permite tomar datos correctamente que luego se pueden usar para determinar las cantidades necesarias (el tamaño angular medio y la mitad de la amplitud). Para determinar esto, Kevin usó un programa conocido como PERDET que está diseñado para ajustar curvas sinusoides a oscilaciones en estrellas variables. ¿Algún programa que pueda ajustar tales curvas a puntos de datos usando un?2 ajuste o un análisis de Fourier sería adecuado para este fin.
A partir de dichos programas, una vez que se determina el tamaño angular medio y la amplitud media, su relación proporciona la excentricidad. Para el experimento de Kevin, encontró un valor de 0.039 ± 0.006. Además, el período que determinó de perigeo a perigeo fue de 27.24 ± 0.29 días, lo cual está en excelente acuerdo con el valor aceptado de 27.55 días.